Honda Civic vs. Jeep Cherokee – Gas Savings
So I recently replaced my aging 91 Isuzu Rodeo with a 91 Honda Civic. Although they were the same model year, the Isuzu had far more mileage (250k) than it was really built fore. So now Sharyn and I have two vehicles: 94 Jeep Cherokee and 91 Honda Civic LX. The Jeep gets around 18 mpg and we recently clocked the Honda on a long trip at 35 mpg. I bought the Honda for $2500 and then spent around $500 on maintenance and taxes, etc. The Isuzu was getting old so we didn’t trust it for long trips and kept driving the Jeep. But now we will be using the Honda. We have already noticed huge savings.
The Question
If the Honda gets 35 mpg and the Jeep gets 18 mpg and I had to spend the extra $3000 on the Honda, how many miles will we have to drive to save $3000 in gas?
The Answer
First off, this is a fun problem for anyone to do if they want to come up with the payback time for upgrading to a more fuel-efficient vehicle. That being said, let’s solve this with a little algebra. The price of gas is going to very and it would be nice to know the distance needed under several different prices so we will set our independent variable, x, to gas price in dollars per gallon and our dependent variable, y, to distance traveled in miles.
I like visually pleasing answers so I chose to create a graph of the curve where the savings is equal to $3000. To do this, we first invert the miles per gallon values to find the gallons per mile.
The gallons per mile multiplied by cost per gallon give us the cost per mile for each vehicle. Unit math is shown on the right in brackets. You can see how the gallons cancel each other out.
The above equations are generalized for mileage, m, and cost, x. The difference between the cost per mile for the Jeep and the Honda can be calculated and then simplified with some factoring giving us the savings per mile. Multiplying this by the number of miles traveled, y, gives us the total savings for y miles.
So back to the original question of saving $3000. If we flip the equation around and replace the “savings for y miles” with the $3000 and then take a few steps to make the formula easier to read, we can plot and interpret the results.
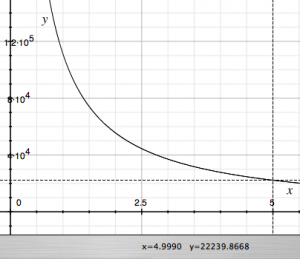
Now substituting the numbers in for the mileage of the Jeep and the Honda and plotting the result, we get a hyperbola. Below, you can see the data point near $3.00 per gallon for x which reads out at approximately 37,000 miles for y.
Now what is fun is that we can see the relationship between how many miles it would take to save $3000 in gas at different prices. Here are a few examples for $2.00 per gallon on the left and $5.00 per gallon on the right.
Taking my equation, you can put in numbers for your cars and compare savings. Here’s an equation to work with:
The output, y, will be the number of miles you need to travel in the vehicle with better mileage to save your desired input at the designated price per gallon.


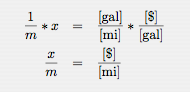

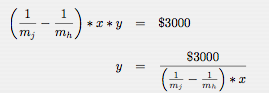


You are amazing and crazy! I just loved this. I get carried away all the time with little math quizzes and things. When I was camping I spent a long period of time watching the river and undercurrents predicting why and when a current took place where, and why it affected future currents and where and what time exactly. There were complicated patterns going on. When I realized how long I’d spent doing this I had to laugh at myself right out loud. I wondered what in the heck the other campers must of thought of this lady so immersed in whaching under currents, running up and down, back and forth. I’m not sure other people notice or care! 🙂 Of course your equation here has real value and mine was pure entertainment! Love you Darrell. You’re one of a kind.
Oh sweet! I’m planning on replacing my aging 94 Beretta soon, and I was (briefly) mulling about how to go about solving this algebra. I hadn’t even gotten to the point of realizing the equation must have two variables. Maybe I saw something shiny… I like shiny things, so use flot to conjure us up a calculator! http://code.google.com/p/flot/
To Lorna: (Hello! it’s been forever!) I wholly believe your musing over the river currents has a type of “real value” of an intrinsic richness such that it cannot ever be compared or converted in any way monetarily. There are systems of beautiful wonder and there are systems of material possession — and ever the twain shall be.
— Nate
Why thank you Nate! Good to hear from you. Sounds like you are well.
Oh, and good luck with the new shining thing!
I guess nobody really checked my math. I just noticed a “typo” in my final equation. It should divide by x ($/gal) instead of multiplying. Whoops!